백준 16947 서울 지하철 2호선 - C++

 

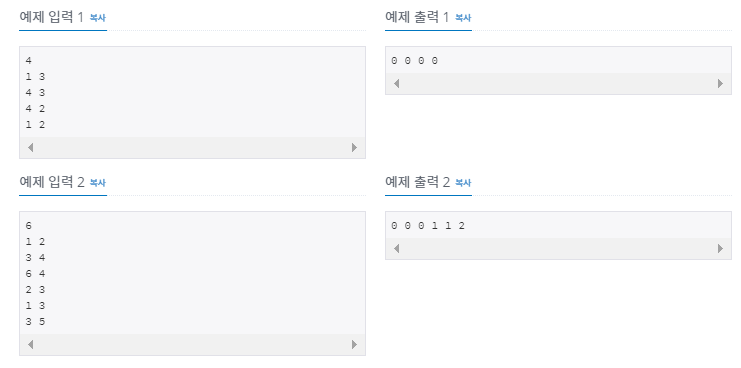
접근

 

1. 순환선에 속하는 정점 파악

2. 순환선에 연결되어 있는 정점들의 최소거리를 구하기

 

순환선을 어떻게 구할지 부터 알아보면 다음과 같다.

순환선은 DFS를 이용하여 구할 수 있다.

먼저, 사이클을 형성하려면 최소 3개의 정점이 연결되어 있어야 한다. 

그리고 1에서 시작한 정점이 다시 1로 돌아와 사이클을 형성하려면 3번의 이동이 필요하다.

사이클 형성 시 사이클에 속하지 않은 정점은 제외해주기 위해 사이클이 만들어질 때 시작 정점을 return값으로 주어야 한다. 

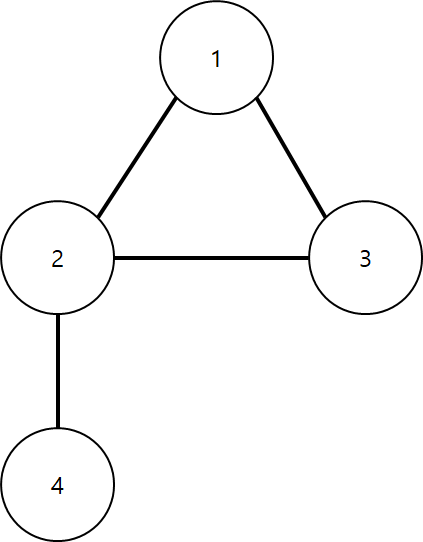
예를 들어, 1 -> 2 -> 3 -> 1 탐색이 되었다고 하면 1 재방문시 이동거리가 3이어서 사이클이 형성된다. 그렇다면 return 하면서 cycle 기록을 해준다면 문제가 없다.

만일 4 -> 2 -> 1 -> 3 -> 2순으로 간다고 하면 2 방문 시 사이클이 형성되고 return 하면서 cycle을 기록해주는데 이떄 4도 사이클에 기록된다.

따라서 사이클 형성 시 사이클의 시작 정점을 return으로 주고 사이클을 기록한다. 사이클 기록을 하다가 return 값으로 받은 시작 정점과 동일한 노드라면 return으로 -1같은 값을 주어 사이클이 끝났음을 알려준다. 

위의 사실을 토대로 조건식을 완성하면 다음과 같다. 

 

vector<int> A[3001];
// 0이면 방문 안함 1이면 방문 2면 사이클에 포함
int check[3001]; 
int dist[3001];

// return 값은 사이클 형성 시작 정점의 번호
int dfs(int node, int cnt){
    // 방문한 정점이라면 사이클이 되는지 확인
    if(check[node] == true){
        if( cnt - dist[node] >=3 ) return node;
        else return -1;
    }
    check[node] = 1;
    dist[node] = cnt;
    // 인접정점 순회
    for(int i=0; i<A[node].size(); i++){
        int nextNode = A[node][i];
        int cycleStartNode = dfs(nextNode, cnt+1);
        // 시작 정점의 번호면
        if ( cycleStartNode != -1) {
            check[node] = 2;
            //사이클에 해당하지 않으면 check에 사이클로 기록하지 않기 위함
            if(node == cycleStartNode) return -1;
            else return cycleStartNode;
        }
        
    }
    return -1;
}

 

마지막으로, BFS를 이용하여 각 정점의 최소 거리를 구한다.

어떤 정점이 순환선에 속해 있으면 거리가 0이고 지선에 속해 있는 정점은 순환선의 한 정점에서 시작하여 거리를 구해야한다.

순환선에 있는 정점을 모두 q에 집어 넣고

지선에 연결되어 있는 순환선의 정점에서 부터 출발하면 모든 정점의 최소 거리를 구할 수 있다. 

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

vector<int> A[3001];
// 0이면 방문 안함 1이면 방문 2면 사이클에 포함
int check[3001]; 
int dist[3001];

// return 값은 사이클 형성 시작 정점의 번호
int dfs(int node, int cnt){
    // 방문한 정점이라면 사이클이 되는지 확인
    if(check[node] == true){
        if( cnt - dist[node] >=3 ) return node;
        else return -1;
    }
    check[node] = 1;
    dist[node] = cnt;
    // 인접정점 순회
    for(int i=0; i<A[node].size(); i++){
        int nextNode = A[node][i];
        int cycleStartNode = dfs(nextNode, cnt+1);
        // 시작 정점의 번호면
        if ( cycleStartNode != -1) {
            check[node] = 2;
            //사이클에 해당하지 않으면 check에 사이클로 기록하지 않기 위함
            if(node == cycleStartNode) return -1;
            else return cycleStartNode;
        }
        
    }
    return -1;
}


int main()
{
    int N;
    cin >> N;
    // 인접 리스트 값 할당
    for(int i=1; i<=N; i++){
        int a,b;
        cin >> a >> b;
        A[a].push_back(b);
        A[b].push_back(a);
    }
    
    //사이클 찾기 
    dfs(1, 0);
    
    
    queue<int> q;
    // 사이클 값은 0 나머지는 -1
    for(int i=1; i<=N; i++){
        if(check[i] == 2){
            dist[i] = 0;
            q.push(i);
        } else {
            dist[i] = -1;
        }
    }
    
    while(!q.empty()){
        int node = q.front(); q.pop();
        for(int i=0; i<A[node].size(); i++){
            int nextNode = A[node][i]; 
            // 사이클이 아닌 정점만 탐색
            if(dist[nextNode] == -1){
                q.push(nextNode);
                dist[nextNode] = dist[node] + 1;
            }
        }
    }

    for(int i=1; i<=N; i++){
        cout << dist[i] << ' ';
    }
    cout << '\n';
    return 0;
}