백준 1759 암호 만들기 - C++

 

접근

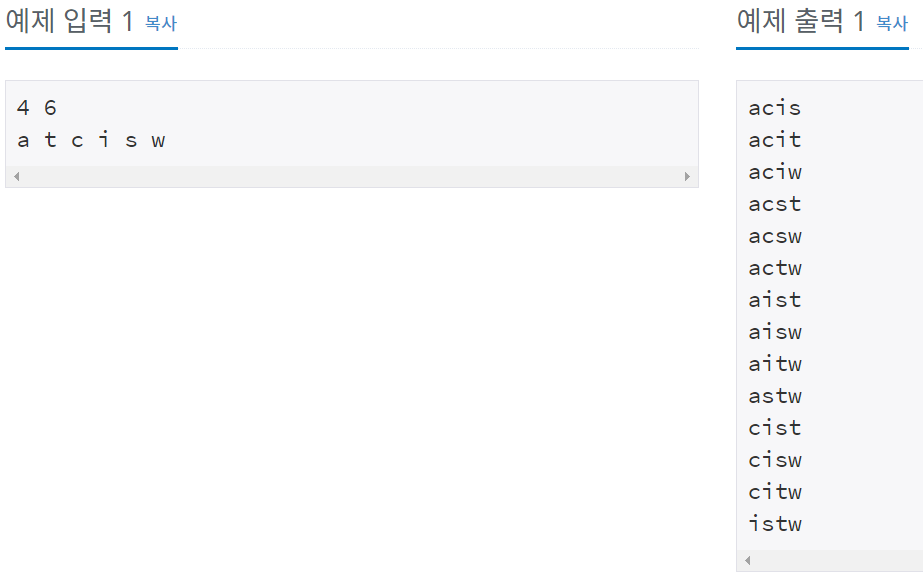
이전에 풀었던 N과 M 문제와 매우 유사하다 다만 조건이 모음과 자음의 개수에 따라 결과가 달라지는 것 정도

우선, 위에 보이는 출력 처럼 문자를 오름차순으로 보여주려면 입력 받은 값에 대해 정렬을 하고 시작하면 빠르다.

 

입력된 문자가 정렬 되었다면 이제 조건에 만족하는 경우의 수를 구해준다.

* 조건은 중복 없이 오름차순이고 만들어진 문자열은 모음 1개 이상 자음 2개 이상을 포함한다.

#include <iostream>
#include <map>
#include <algorithm>
using namespace std;
map<char, bool> vowel;
int L, C;
char alpha[15];
char arr[15];
void re(int idx, int begin, int vowelCnt){
    if(idx == L){
        int consonant = L-vowelCnt;
        if(consonant >= 2 && vowelCnt >= 1 ){
            for(int k=0; k<L; k++){
                cout << arr[k];
            }
            cout << '\n';
        } 
        return;
    }
    
    for(int i=begin; i<C; i++){
        char curAlpha = alpha[i];
        if(vowel.count(curAlpha) == 1) vowelCnt++;
        arr[idx] = alpha[i];
        re(idx+1, i+1, vowelCnt);
        if(vowel.count(curAlpha) == 1) vowelCnt--;
    }
    return;
}

int main(){
    cin >> L >> C;
    for(int i=0; i<C; i++){
        cin >> alpha[i];
    }
    vowel.insert(make_pair('a',true));
    vowel.insert(make_pair('e',true));
    vowel.insert(make_pair('i',true));
    vowel.insert(make_pair('o',true));
    vowel.insert(make_pair('u',true));
    
    sort(alpha, alpha+C);

    re(0,0,0);
    return 0;
}

 

위의 방법대로 조건에 만족하는 모든 경우의 수를 구해도 되고 각 자릿수가 사용될지 안될지를 결정하여 풀 수도 있다. 

[a,c,i,s,t,w]가 있을 때 

a가 사용 또는 미사용 c가 사용 또는 미사용 이런식으로 풀 수도 있다.

그렇다면 각각은 사용될 수도 있고 사용되지 않을 수도 있기 때문에 2의 6제곱만에 구할 수 있다.

#include <iostream>
#include <map>
#include <algorithm>
using namespace std;
map<char, bool> vowel;
int L, C;
char alpha[15];
char arr[15];
void re(int idx, int alphaIdx, int vowelCnt){
    if(idx == L){
        int consonant = L-vowelCnt;
        if(consonant >= 2 && vowelCnt >= 1 ){
            for(int k=0; k<L; k++){
                cout << arr[k];
            }
            cout << '\n';
        } 
        return;
    }
    if(alphaIdx == C) return;
    
    char curAlpha = alpha[alphaIdx];
    //Yes
    if(vowel.count(curAlpha) == 1) vowelCnt++;
    arr[idx] = curAlpha;
    re(idx+1, alphaIdx+1, vowelCnt);
    if(vowel.count(curAlpha) == 1) vowelCnt--;
    //No
    re(idx, alphaIdx+1,vowelCnt);

    return;
}

int main(){
    cin >> L >> C;
    for(int i=0; i<C; i++){
        cin >> alpha[i];
    }
    vowel.insert(make_pair('a',true));
    vowel.insert(make_pair('e',true));
    vowel.insert(make_pair('i',true));
    vowel.insert(make_pair('o',true));
    vowel.insert(make_pair('u',true));
    
    sort(alpha, alpha+C);

    re(0,0,0);
    return 0;
}